法律与王权：中世纪英国法治观念的嬗变及其内在逻辑

      很多学生在面对导数综合题时，一般都会考虑原有函数的定义域，然后就对原有函数求导数，或根据问题情境，构造一个函数再求导数.那么为什么要求导？求导的目的是什么？所求得的导数便于后续研究吗？所研究问题的本质是要研究函数的什么性质？学生对诸多问题可能没有考虑清楚，更多的还是模式化解题.不可否认，函数的单调性是函数的最重要性质之一.导数最直接的应用就是研究函数的单调性，但不是所有的问题都要研究函数的单调性.如果需要研究函数的单调性，而导数含参数且特别复杂，分类讨论的分界点该如何确定呢？很多学生求导数之后，就陷入不知所措、无从下手、停滞不前的窘境，更谈不上找到解决问题的突破口了.

      例如，2019年全国I卷理科20题的第（Ⅱ）问，学生就遇到很大的挑战.

      （2019年全国I卷理20节选）已知函数f（x）=sinx-ln（1+x）.

      证明：f（x）有且仅有2个零点.

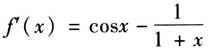      分析 如果盲目从导数入手，导数的零点不易发现，进而很难得出原函数的单调区间，也就无法判断出原函数值正负的变化情况，问题就很难解决.由于找不到突破口，解题陷入困境.若能抓住零点问题的本质，结合函数零点的概念，进而考虑方程sinx=ln（1+x）根的情况，也就转化为y=sinx与y=ln（1+x）的交点情况，画出两者图象（如右上图），解题方向一目了然，即使不作出函数图象，因为一般函数的零点与函数值的正负有关联，若能有观察原有函数的函数值变化的意识，就可能发现f（0）=0，所以x=0是f（x）的一个零点.再做一下试验，发现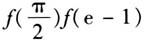＜0，根据要证明的结论可断定函数在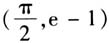上有1个零点，这样解题的目标就确定了，也就是只需证f（x）在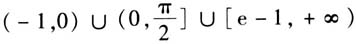上无零点，在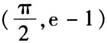上有且仅有1个零点.解答略.由此可以看出，关注原有函数的性质对问题解决是多么重要.

      

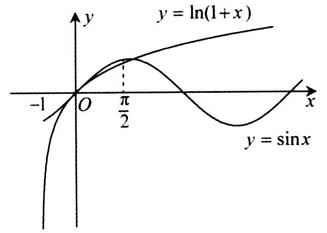      优先考虑函数的定义域，其实这就是关注原有函数的一种性质.但我们不能仅仅局限这一点，也不能求导数之后就抛弃了原有函数.我们要根据所求问题的本质，关注原有函数以及导函数的相关性质，找到问题的突破口，再利用导数这一工具解决问题.笔者结合自己的教学实践，重点谈一谈在解决函数与导数综合问题中除关注定义域外，还应关注原有函数的哪些性质？下面结合例子从四个方面加以说明.限于篇幅，所举例子均节选一个问题进行解释，以此来感受关注原有函数本身的某些性质对所研究问题带来的优化.

      一、关注多项式或函数值整体的正负，明晰问题本质

      关注多项式或函数值整体的正负对证明不等式、函数零点、恒成立或有解问题至关重要.

      

      点评 本题没有用导数研究函数的最值来证明不等式，问题的解决根本就没用到导数这一工具.函数不等式的证明，不一定要构造函数，通过研究单调性等性质，再求出函数的最值达到论证的目的.函数不等式证明的数学本质还是作差，看差值的正负即可.本题根据题目的结构特征，用适当的转化、代数变形、放缩等手段就能达到论证的目标，从而问题得以快速解决.上面两种解法需要较高的数学素养，给学生带来震撼，是去除模式化的好素材.特别是“证法一”关注了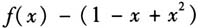整体的正负.还有什么时候要关注多项式或函数值整体的正负呢？

      

      点评 函数最值或极值的正负某种程度决定该函数有无零点问题，这是零点问题的一个基本认识.解法一就是依据这个认识.但极值的正负不好判断，有时需要一定的技巧.更朴素的一个道理是：“函数在某区间上恒正或恒负，则函数在此区间上无零点”.若知道函数在某区间上恒正或恒负，就无需关注它在此区间上的单调性情况，更不用关注极值的正负，所以解法二是站在整体的角度看问题，解法当然更加简洁.在教学时，我们可以采取这种对比教学，既落实基本解法，又培养学生观察、整合、创新的意识，使学生对问题本质有更深刻的思考.